An effect similar to Peukert's effect during charging. Not commonly known about.

You now know all about Peukert's effect during discharging. How it affects available run times for different discharge rates etc. You can even calculate it's effect with quite high accuracy. Or can you? And do you know what causes it? And are you aware that a similar effect takes place during charging thus making amp hours counters even more prone to errors?

Peukert's effect is the result of 2 quite distinct properties of a battery. These two properties combine to give an effect that is quantifiable by use of Peukert's equation.

But Peukert's equation does not explain what causes the effect. It merely quantifies it. Yet once the reason for the effect is known, it becomes clear why simply entering a Peukert's exponent for a particular battery is always going to lead to problems in the future as the battery ages. Yet this is what amp hours counters attempt to do. Which is another reason why they do not work.

The two factors that affect, and therefore define, Peukert's exponent for any particular battery are:-

A. The internal resistance of the battery due to the resistance at the interface between the lead plates and the electrolyte and the internal resistance of the battery due to the actual resistance of the electrolyte itself.

and....

B. The resistance of the electrolyte as a whole i.e inlcuding the bubbles and contaminants within it.

The battery has other components that affect the internal resistance, such as the conductors, the framework for the lead plates etc, but these remain extremely low (in relation to the two points mentioned above - thus they have almost no effect) and constant (thus they have no change in effect between flat and fully charged) during the life and cycle of the battery.

During discharge, the plates turn to lead suplhate. Lead sulphate does not conduct electricity very well. Therefore as the battery discharges, there is less lead dioxide (in the positive plate) and less lead (in the negative plate) in contact with the electrolyte. Less contact area obviously means less conductive path = higher resistance. So as the battery becomes discharged, the internal resistance rises.

The electrolyte, at fully charged state, is a quite high concentration of sulphuric acid. Sulphuric acid is an excellent conductor. As the battery discharges, the electrolyte becomes weaker (this is what drives the battery). Eventually, at the completelty flat state, the electrolyte consists entirely of pure water. Pure water is an extremely poor conductor.

So as you can see from the above the internal resistance rises as the battery discharges. It is exactly this rise in resistance that prevents the battery from producing the same high currents that it is capable of when fully charged.

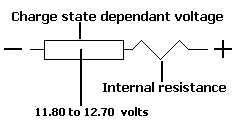
Now it's time to have a look at a very simple battery model. This is a first representation of a battery used for simulation. Note that the models used in SmartGauge are approximately 1000 times more complex than this but this serves it's purpose for this discussion.

The current from the voltage source has to pass through the internal resistance of the battery in order to reach the loads. Let's say that the battery is fully charged so the voltage source is fixed at 12.70 volts. Let's also say the internal resistance is 0.005 Ohms.

If we now put a load on the battery of 1 Ohm resistance. We can calculate that the 12.70 volts is dropped across 1.005 Ohms (the 1 Ohm load plus the 0.005 Ohms internal resistance).

According to Ohm's law (V=I*R or I = V/R in this case) a current of 12.70/1.005 amps will flow. This calculates to 12.64 amps. So our 1 Ohm load has 12.64 amps through it and so does the 0.005 Ohms internal resistance.

Again using Ohm's law we can therefore calculate that the load will have 12.64 amps * 1 Ohms = 12.64 volts across it. The power in the load is therefore 12.64 amps * 12.64 volts = 159.7 watts.

By the same reasoning the internal resistance has 12.64 * 0.005 Ohms = 0.063 volts dropped across it. The internal resistance therefore dissipates 12.64 amps * 0.063 volts = 0.8 watts.

So due to the internal resistance of the battery, The terminal voltage dropped to 12.64 volts. The heavier the load, the more the terminal voltage will drop.

Due to the internal resistance of the battery, the battery dissipated 0.8 watts. This it dissipates (mostly) as waste heat. This is why batteries get warm when they are worked. And the harder they are worked, the warmer they get.

And the higher the load, the more power will be dissipated in the internal resistance.

So you can see that the more current we draw from the battery, the more power will be wasted internally in the internal resistance. The problem is that this resistance is not constant. It increases (due to chemical effects) exponentially with increasing load. This is one factor that causes Peukert's effect (and explains why Peukert's effect is exponential rather than linear). The heavier the discharge current, the more power is wasted inside the battery, thus there is less power available to run external loads.

As explained above, as the battery becomes discharged further, the internal resistance rises further, thus the effect becomes greater as the battery is discharged.

And also as explained above, as the battery ages, more and more sulphate becomes stuck on the plates, thus the internal resistance rises as the battery ages. The electrolyte also becomes contaminated with corroded conductors and crystalised sulphate. The electrolyte also becomes weaker. Thus Peukert's effect increases as the battery ages, thus Peukert's exponent increases as the battery ages.

Entering Peukert's exponent for a battery type lifted from the battery data will only work when the battery is new. As the battery ages, Peukert's exponent needs to be increased. But the only way to get Peukert's exponent for a battery type is to discharge very deeply at varying discharge rates and calculate the results. Yet another reason why amp hours counters do not work.

If that was all there was to it, the effect would be relatively simple to calculate and Peukert's equation would probably not be required. A much simpler formula would suffice.

But there is more to it. At heavier discharge currents, the chemical reactions take place much faster and this produces gas bubbles in the electrolyte. So although the actual resistance of the electrolyte remains the same for a given charge state and battery age/condition, the overall resistance increases depending upon the discharge rate due to the bubbles in the electrolyte.

So we actually have 3 separate effects that combine to produce Peukert's effect:-

A. The resistance of the battery due to the interface between the plates and the electrolyte.

B. The resistance of the electrolyte itself and......

C. The bulk resistance of the electrolyte due to the bubbles being produced within it.

These three effects combine to produce the overall Peukert's exponent for a particular battery.

And Peukert's equation does a very good job of calculating the overall effect, if Peukert's exponent is correct. Which it won't be once the battery has aged somewhat.

But now to the main point of this document.

The three effects shown above also apply during charging. But they are impossible to calculate because of the way charging causes the chemicals reactions to take place. As they are impossible to calculate, amp hours counters make no attempt at doing so. Yet the effects can be dramatic.

It is often stated (by people who really should know better) that as a battery approaches full charge, the internal resistance rises sharply and this causes a fall in the charge current. This is actually only half the story.

The reason the charge current falls is two-fold:-

Firstly, at a fixed charge voltage, as the battery approaches full charge, the "at rest" voltage of the battery rises sharply. Therefore there is less voltage difference between the charge voltage and the battery voltage. Less voltage difference obviously means less charge current.

Secondly, as the battery approaches full charge state, the chemical reactions within the battery change. Less energy goes into recharging the battery (i.e. converting lead sulphate back into sulphuric acid) and more goes into producing gasses. This is why batteries begin to gas vigorously once they approach or reach a fully charged state. In fact this is one of the old methods technicians used to use to detect when a battery was fully charged.

This sudden burst of gasses within the electrolyte increases the bulk resistance of the electrolyte which causes a further fall in charge current.

So the fall in charge current is not simply due to the increased internal resistance. Also, the statement that the internal resistance rises as the battery approaches the fully charged state is somewhat misleading. The actual internal resistance falls as the battery reaches higher charge states. As soon as the charge source is removed, bubble production ceases, and the internal resistance falls to a very low level. Thus switching the charger back on will, once again, cause a high charge current until bubble production restarts. But if the charge current is high until bubble production restarts, that must mean that the battery is not fully recharged, otherwise the current would remain low. This can cause an amp hours counter to decide a battery is fully charged well before it actually is.

These effects, in conjunction with the same effects that cause Peukert's effect (during discharge) combine to produce a set of parameters that simply cannot be predicted or calculated when relying upon counting amps in and out of the battery.

Some amp hours counters attempt to wait until the battery charge current has fallen to a certain level then use this as the deciding factor that the batteries are fully charged.

This is fraught with difficulties.

A common figure is 2% of the battery capacity. This means that when charging a 100 amp hour battery, when the charge current falls below 2 amps the batteries are deemed to be full.

There are 3 problems here.

Firstly, as explained above, the charge current may fall to a very low level, due to gas production, well before the batteries are fully charged.

Secondly, the charge current will depend upon the charge voltage but not in a linear way. At around 14.3 volts (for a wet cell) the charge current will be the highest. Either side of this charge voltage the current will drop. A reduction in charge voltage will reduce the charge current due to the drop in voltage difference between the charger and the "at rest" voltage of the battery. An increase in charge voltage will cause a reduction in charge current due to the increase in gas production and consequent increase in internal resistance. But the exact peak charge current point is temperature dependant, battery condition dependant, state of charge dependant and also subject to a time delay. Amp hours counters do not take the voltage, temperature or time delay into consideration (because there is no way of doing so), and cannot take the state of charge into consideration (because they have no idea what the state of charge is unless the operator tells them) when deciding that the batteries are fully charged according to the drop in charge current.

Finally, whatever final figure is chosen, be it 2%, 3%, 5% or whatever, depending upon the age of the battery, the charge current may never fall below this level because as the battery ages, and it becomes less efficient, the charge current may remain above this level as a result of inefficient chemical reactions doing nothing more than producing gasses.

So in summary, the charge current may fall below this level, due to gas production, well before the batteries are fully charged.

The charge current may never fall below this level, even though the batteries are fully charged, due to inefficienct chemical reactions as a result of battery ageing.

All these effects combine to produce something that is, quite simply, totally incalculable. If it cannot be calculated, then it certainly cannot be predicted.